Assignment 4

April 2, 2021 12 minute read

과제 4

과제	4
점수	0
제출	False

0. 연습문제 해설

0.1. 과제 2. 연습문제

학번이 20219999인 경우,

 >> MAS109_assign2_ex1(20219999)

를 입력하여 다름과 같은 매개변수 함수 \(x,\, y\)를 얻을 수 있습니다.

eq1

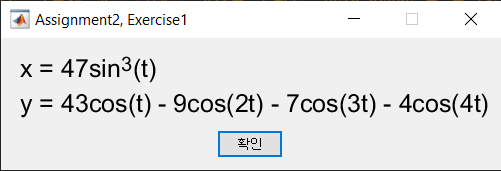
매트랩 명령어 plot를 이용하여, 범위 \(-\pi \le t \le \pi\)에서 \((x, \, y)\)가 나태내는 그래프를 그릴 수 있습니다.

 t = -pi:0.01:pi;
 x = 47 * sin(t).^3;
 y = 43 * cos(t) - 9 * cos(2 * t) - 7 * cos(3 * t) - 4 * cos(4 * t);

 figure;
 plot(x, y, 'r');        % plot the graph of parametric x and y
 grid on; axis tight;

MATLAB result

eq1

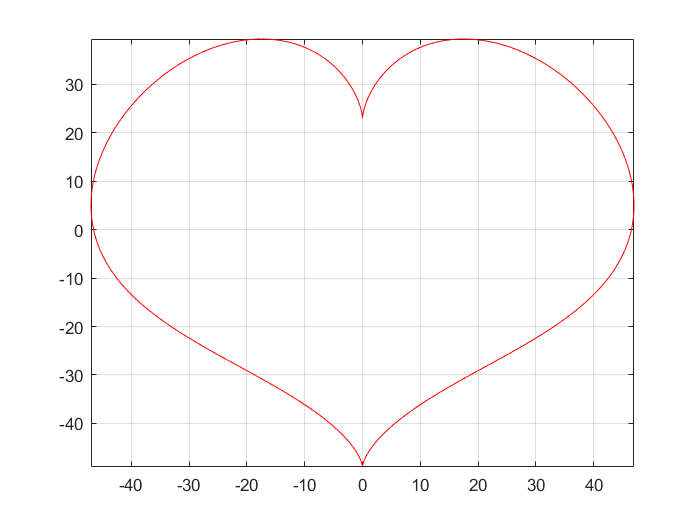
학번이 20219999인 경우,

 >> MAS109_assign2_ex2(20219999)

를 입력하여 다음과 같은 \(x,\,y\)에 대한 함수 \(z\)를 얻을 수 있습니다.

eq1

매트랩 명령어 meshgrid와 mesh(또는 surf)를 이용하여, 범위 \(-1 \le x,\,y \le 1\)에서 \(z\)의 그래프를 그릴 수 있습니다.

해답

 x = -1:0.01:1;              % set range of x, y as [-1, 1]
 y = x;

 [X, Y] = meshgrid(x, y);     % expand x, y to the rectangular grid

 Z = 2 * cos(-7 * X .* Y).^3 + sin(5 * Y).^2 - exp(-X.^2 - Y.^2);

 figure;
 mesh(X, Y, Z);              % plot the graph of parametric x and y
 grid on; axis tight;

MATLAB result

eq2

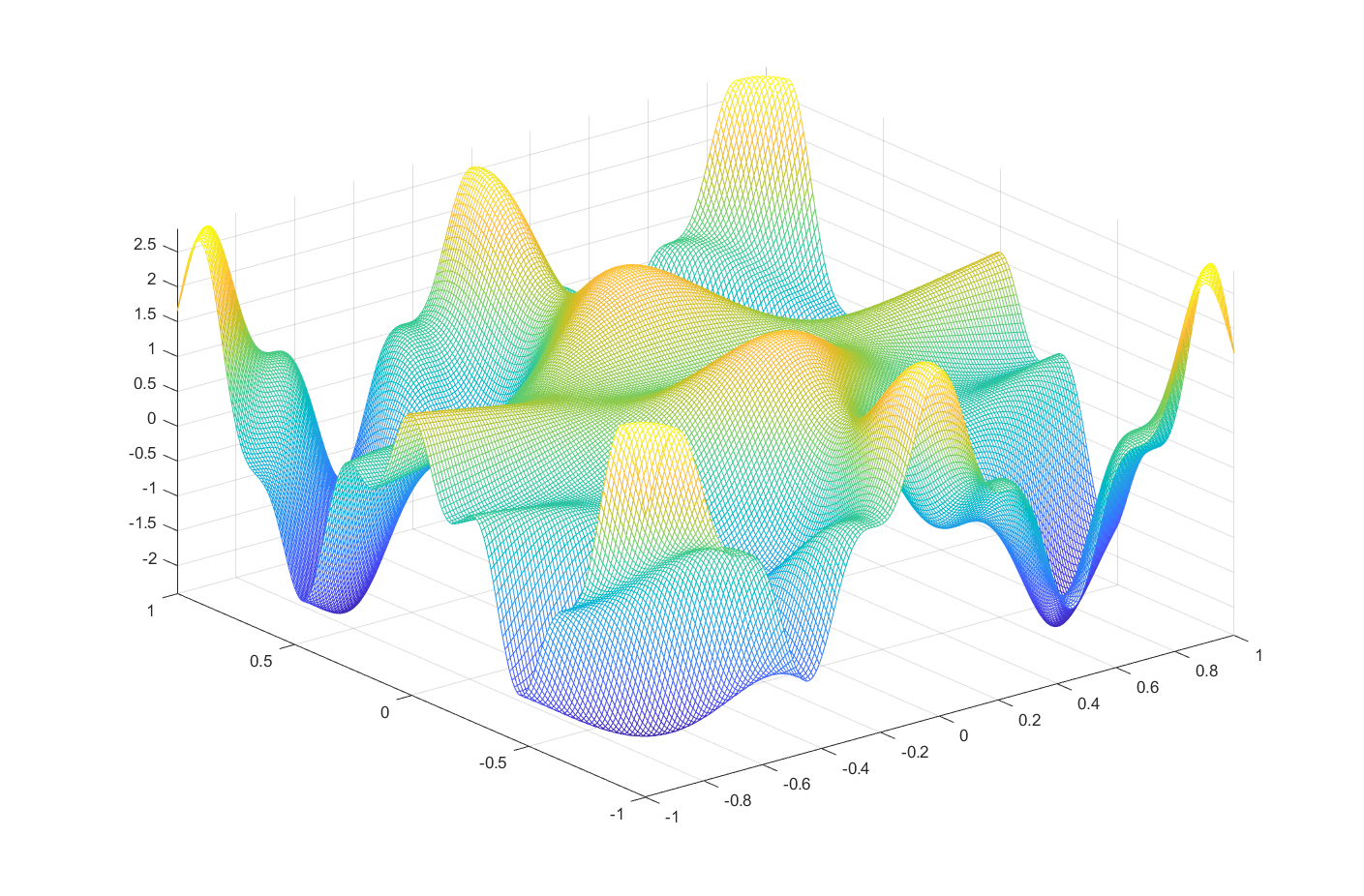
0.2. 과제 3. 연습문제

그래프를 그려서 다음 극좌표계의 교점의 개수를 찾으세요.

\[\begin{cases} r = 1+\cos(k\theta)\\ r = \cos(k\theta)\\ \end{cases}, \qquad \text{where} \quad 0\le\theta\le 2\pi\]

 % Create a linearly-spaced vector of the parameter domain theta
 theta = linspace(0, 2*pi, 200);

 figure(1); clf (1);             % Open a figure window
 for k =1:6
     r1 = 1 + cos(k * theta);    % Calculate the values r1.
     r2=cos(k * theta);          % Calculate the values r2.
     subplot(2, 3, k);
     polarplot(theta, r1, 'b');  % Draw the polar curve r
        
     hold on;
     polarplot(theta, r2, 'r');
     title(sprintf('ex 1: The polar curve r=sin (%d* theta)', k));
 end

MATLAB results

fig

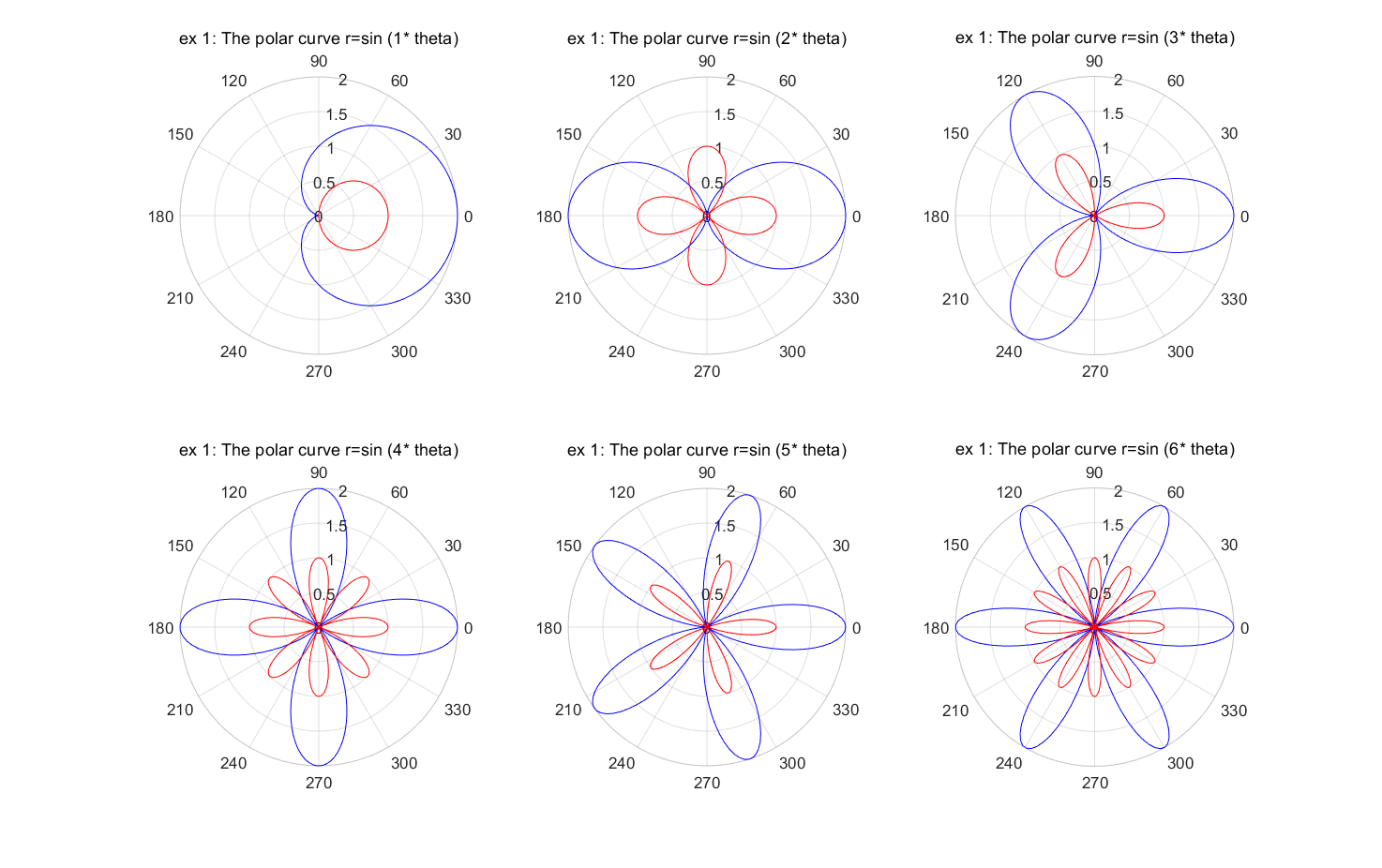
1. `if` 조건문

if 조건문의 핵심은 바로 ‘조건’이 무엇인가 하는 것인데요, 컴퓨터는 어떤 명제가 참인지 거짓인지를 숫자 0, 1로 판별합니다. 조건이 0이면 거짓, 1이면 참인 것이죠. 매트랩에서 이런 조건을 나타내는 방법은 (주로) ‘연산자’를 사용한 ‘조건식’을 사용하는 것입니다. 연산자의 종류는 대표적으로 ==, ~=(같음 연산자)와 <, <=, >, >=(관계 연산자)들이 있습니다. 매트랩 명령창에서,

1 == 1

을 입력하면 매트랩은 ‘참’이라는 뜻으로 1을 출력할 것입니다. 반대로

1 ~= 1

을 입력하면 ‘거짓’이라는 뜻으로 0을 출력하겠죠. 이처럼 두 수(뿐만아니라 두 행렬)간의 비교를 통한 조건식을 작성할 수 있습니다.
(C, C++, Java, Python 등 많은 언어들에서 두 수가 다름을 표현할 때 !=을 사용합니다. 하지만 매트랩의 경우는 ~=을 사용하니, 유의하세요.)

1.1. 간단한 `if` 조건문

if 조건문은 여러가지로 형태로 변형하여 사용할 수 있습니다. 그 중 가장 간단한 형태는 다음과 같습니다.

if <조건>
    <코드>
end

<조건>이 참(1)이면 <코드>를 실행하는 것이죠. 간단한 예를 보면,

x = 3;
if x < 5
    disp("x is less than 5.")
end

x가 숫자 5보다 작으면 알려주는 코드를 작성할 수 있습니다. 만약 첫 줄이 x=6과 같이 변한다면 아무것도 출력되지 않겠죠.

1.2. `if-else` 조건문

if-else 조건문은 두가지 경우의 수를 고려할 수 있는 조건문입니다. 다음과 같은 형태로 사용합니다.

if <조건>
    <코드1>
else
    <코드2>
end

만약 <조건>이 참이면 <코드1>을 실행하고, 그렇지 않으면 <코드2>를 실행하게 되는 것이죠. 예를들어 다음학기 수강신청때, 선형대수학개론이 재미있으면 선형대수학을 수강하고, 재미 없으면 선형대수학을 수강하지 않도록 결심하는 상황을 생각해 보면, 다음과 같이 나타낼 수 있을 것입니다.

MAS109 = input("Was MAS109 fun? Type 1 if it was.");
if MAS109 == 1
    disp("Let's go to take the MAS212");
else
    disp("Yes, it could be, I understand.");
end

변수 MAS109에 1이 저장되었을때와 그 외의 경우로 나누어서 출력문을 바꿀 수 있습니다.

1.3. `if-elseif-else` 조건문

여러가지 조건을 한번에 따져서 각 경우에 맞는 코드를 작동시킬 수 있습니다.

if <조건1>
    <코드1>
elseif <조건2>
    <코드2>
else
    <코드3>
end

이처럼 if-elseif-else조건문은, <조건1>이 참이면 <코드1>을, <조건1>이 거짓이소 <조건2>가 참이면 <코드2>를, <조건1>과 <조건2>가 모두 거짓이면 <코드3>을 실행하도록 작성할 수 있습니다.

2. `continue`와 `break`

continue

if문을 사용하여 반복문 안의 코드를 선택적으로 실행할 수 있습니다. 예를들어, 1부터 100까지의 숫자들 중 홀수만 더하는 문제를 생각해보죠. 사실 이 문제는 if문을 사용하지 않아도 지난시간에 배운 for반복문을 사용하여 쉽게 해결할 수 있습니다.
```
 S = 0;
 for i = 1:2:100
     S = S + i;
 end
 fprintf("S = %d\n", S)
```
다른방법으로도 해결할 수 있을까요? 반복문과 if문, continue를 사용하면 짝수는 건너뛰고 홀수만 반복적으로 더할 수 있습니다. 여기서 continue는 ‘이번 반복’을 건너뛰고 ‘다음 반복’으로 넘어갈 수 있게하는 역할을 합니다.
(사실 이 방법이 더 비효율적이지만, continue함수를 직접 사용해보기 위해 보도록 하겠습니다.)
```
 S = 0;
 for i = 1:100
     if mod(i, 2) == 0
         continue        % skip this iteration
     end
     S = S + i;
 end
 fprintf("S = %d\n", S)
```
break

break는 continue와는 조금 다르게 작동합니다. 반복문 안에서 break를 만나게되면, 현재 진행중인 반복문을 벗어나게 됩니다. 예를들어, 만약 우리가 while문의 조건을 1로 부여하면, 항상 참인 조건이기 때문에 while문은 무한히 반복될 것 입니다. 이렇게 무한히 반복되는 코드를 ‘무한 루프’라고 하는데, 실수로 무한 루프를 생성하게되면 강제로 코드 실행을 종료해야만 하는 상황이 생기게 됩니다. 어찌되었든, 루프 안에서 break를 만나게되면 조건과 상관없이 반복이 종료되고 while문의 end로 이동하게 됩니다.
```
 k = 0;
 while 1
     fprintf("Now k is %d\n", k);
     if k >= 10
         break
     end
     k = k + 1;
 end

 fprintf("Now the while-loop is broken\n")
```

3. `function`의 작성

매트랩의 편집기를 이용하면 스크립트 파일(*.m)을 작성할 수 있다는 건 이미 알고 있을겁니다. 스크립트 파일에 코드를 작성하여 저장해놓으면 원할때마다 불러와서 실행할 수 있습니다. 매트랩에서는 스크립트 파일을 단순 실행하는 것 뿐만 아니라 ‘함수’로 만들어서 입력값과 출력값을 가지도록 저장할 수 있습니다. 매트랩의 함수는 다음과 같은 형식을 가집니다.
(매트랩에서는 명령창에서 함수를 정의할 수 없습니다. 반드시 스크립트 파일로 작성한 뒤 저장하여 사용해야 합니다.)

function [<출력1>, <출력2>, ... ] = <함수이름>(<입력1>, <입력2>, ... )
    <코드>
end

함수는 여러개의 출력과 여러개의 입력을 가질 수 있습니다. 두 수를 입력받아 더하는 함수를 생각해보면:

% mySum.m
function aPb = mySum(a, b)
    aPb = a + b;
end

위 함수를 mySum.m이라는 이름으로 저장한 뒤, 명령창에 mySum(1, 3)을 입력하면 우리가 예상한 결과를 얻을 수 있습니다. 이 경우에는 출력되는 변수가 aPb하나밖에 없기때문에 []를 생략했지만, 여러개의 변수를 출력하는 함수의 경우는 반드시 []를 이용해야 합니다.

% mySumMul.m
function [aPb, aTb] = mySumMul(a, b)
    aPb = a + b;
    aTb = a * b;
end

이 함수역시 스크립트 파일로 저장한 뒤 명령창에서 mySumMul(3, 4)처럼 불러올 수 있습니다. 이 때, 따로 지정하지 않는다면 함수는 항상 첫번째 출력변수(aPb)만을 출력합니다. 만약 두 결과를 모두 출력받으려면, [x, y] = mySumMul(3, 4)와 같이 입력받을 변수들 각각에 대해 대응시켜주어야 합니다.

연습문제

임의의 정사각행렬을 입력받아 행렬식을 출력하는 함수를 작성하세요.
[힌트: 매트랩 함수는 자기 자신을 반복적으로 불러오는 형태로 작성될 수 있습니다. Co-factor 전개가 그 자체로 반복적인 형태를 갖는 걸 기억하세요.]
주어진 행렬의 RREF를 찾는 함수 myRREF를 작성하세요.

임의의 행렬에 대한 RREF를 찾는 함수를 작성하는건 다소 복잡합니다. 여기서는, 3가지 기본행연산 중 ‘두 행의 교환’을 사용하지 않고 가우스 소거법을 적용할 수 있는 행렬들에 대해서만 작동하는 함수를 작성하세요. 교과서 2.1의 연습문에 6 에서 이와같은 행렬을 발견할 수 있습니다.
2번문제를 참고하여, ‘두 행의 교환’을 사용하지 않고 가우스 소거법을 적용할 수 있는 행렬들에 대하여 \(LU\)-분해를 하는 함수를 작성하세요.

Assignment 4

Assignment	4
Score	0
Submission	False

0. Solution to exercises

0.1. Exercises, assignment 2

Let ID number is 20219999. By entering the following codes in command window,

 >> MAS109_assign2_ex1(20219999)

you can get parametric functions \(x,\, y\).

eq1

Using the MATLAB command plot, you can plot the graph represented by \((x, \, y)\) in the range \(-\pi \le t \le \pi\).

 t = -pi:0.01:pi;
 x = 47 * sin(t).^3;
 y = 43 * cos(t) - 9 * cos(2 * t) - 7 * cos(3 * t) - 4 * cos(4 * t);

 figure;
 plot(x, y, 'r');        % plot the graph of parametric x and y
 grid on; axis tight;

MATLAB result

eq1

Let ID number is 20219999. By entering the following codes in command window,

 >> MAS109_assign2_ex2(20219999)

You can get the function \(z\) w.r.t. the variables \(x,\,y\) like the following.

eq1

Using the MATLAB commands meshgrid and mesh (or surf), you can graph \(z\) in the range \(-1 \le x,\,y \le 1\).

 x = -1:0.01:1;              % set range of x, y as [-1, 1]
 y = x;

 [X, Y] = meshgrid(x, y);     % expand x, y to the rectangular grid

 Z = 2 * cos(-7 * X .* Y).^3 + sin(5 * Y).^2 - exp(-X.^2 - Y.^2);

 figure;
 mesh(X, Y, Z);              % plot the graph of parametric x and y
 grid on; axis tight;

MATLAB result

eq2

0.2. Exercises, assignment 3

Find the number of intersections of the polar system

\[\begin{cases} r = 1+\cos(k\theta)\\ r = \cos(k\theta)\\ \end{cases}, \qquad \text{where} \quad 0\le\theta\le 2\pi\]

Solution

 % Create a linearly-spaced vector of the parameter domain theta
 theta = linspace(0, 2*pi, 200);

 figure(1); clf (1);             % Open a figure window
 for k =1:6
     r1 = 1 + cos(k * theta);    % Calculate the values r1.
     r2=cos(k * theta);          % Calculate the values r2.
     subplot(2, 3, k);
     polarplot(theta, r1, 'b');  % Draw the polar curve r
        
     hold on;
     polarplot(theta, r2, 'r');
     title(sprintf('ex 1: The polar curve r=sin (%d* theta)', k));
 end

MATLAB results

fig

1. `if` conditional statement

The key to the if conditional statement is what the ‘condition’ is, and the computer determines whether a certain proposition is true or false as the numbers 0 and 1. If the condition is 0, it is false, and if the condition is 1, it is true. The way to express these conditions in MATLAB is to use’conditional expressions’ using ‘operators’. Representative types of operators are ==, ~= (equality operator), <, <=, >, and >= (relational operator). In the MATLAB command window, if you enter

1 == 1

then MATLAB will output ‘1’, meaning’True’. Contrary, if you enter

1 ~= 1

then it will output ‘0’, meaning ‘false’. In this way, You can write a conditional expression by comparing two numbers like this.
(Many languages such as C, C++, Java, and Python use != when expressing the difference between two numbers. However, in the case of MATLAB, ~= is used, so be careful.)

1.1. a simple `if` statement

if statement can be used in various forms. The simplest of them is:

if <condition>
    <code>
end

If <condition> is true (1), then <code> is executed. Looking at a simple example,

x = 3;
if x < 5
    disp("x is less than 5.")
end

You can write code that tells you if x is less than the number 5. If the first line changes like x=6, nothing will be printed.

1.2. `if-else` statement

if-else statement can take into account two cases. It is used in the following form.

if <condition>
    <code1>
else
    <code2>
end

If <condition> is true, <code1> is executed, otherwise <code2> is executed. For example, when enrolling for a course next semester, you could decide to take Linear Algebra if you are interested in the Introduction to Linear Algebra, and if it is not, you could not decide to take Linear Algebra. This can be written in the code:

MAS109 = input("Was MAS109 fun? Type 1 if it was.");
if MAS109 == 1
    disp("Let's go to take the MAS212");
else
    disp("Yes, it could be, I understand.");
end

1.3. `if-elseif-else` statement

You can run the code for each case by considering several conditions at once.

if <condition1>
    <code1>
elseif <condition2>
    <code2>
else
    <code3>
end

Here, <code1>is executed if <condition1> is true, <code2> is executed if <condition1> is false and <condition2> is true, and <code3>is executed if both <condition1> and <condition2> are false.

2. `continue`and `break`

continue

You can use the if statement to selectively execute the code inside the loop. For example, consider the problem of adding only odd numbers from 1 to 100. In fact, this problem can be easily solved by using the for loop we learned last time without using the if statement.
```
 S = 0;
 for i = 1:2:100
     S = S + i;
 end
 fprintf("S = %d\n", S)
```
Could it be solved in other ways? If you use a loop, if statement, and continue, even numbers can be skipped and only odd numbers can be added repeatedly. Here, continue allows you to skip the ‘this iteration’ and move on to the ‘next iteration’.
(Actually, this method is more inefficient than the before, but let’s look at it to try the continue directly.)
```
 S = 0;
 for i = 1:100
     if mod(i, 2) == 0
         continue        % skip this iteration
     end
     S = S + i;
 end
 fprintf("S = %d\n", S)
```
break

break works a little differently than continue. When it encounters break in the loop, it breaks the loop in progress. For example, if we give the condition of the while to 1, the while iterates infinitely because the condition is always true. Loop that repeats infinitely like this is called an ‘infinite loop’, and if you accidentally create an infinite loop, there is a situation where you have to forcibly terminate execution of the code. Anyway, in any loops, when a break is encountered, the loop ends regardless of the condition and moves to the end of the while statement.
```
 k = 0;
 while 1
     fprintf("Now k is %d\n", k);
     if k >= 10
         break
     end
     k = k + 1;
 end

 fprintf("Now the while-loop is broken\n")
```

3. `function` file

You probably already know that you can create script files (*.m) using MATLAB’s editor. If you write and save the code in the script file, you can load it and run it whenever you want. In MATLAB, you can not only simply execute a script file, but also make it a ‘function’ and save it to have input and output values. MATLAB functions have the following format: (You cannot define a function in the command window in Matlab. You must write it as a script file and save it for use.)

function [<output1>, <output2>, ... ] = <function name>(<input1>, <input2>, ... )
    <code>
end

Functions can have multiple outputs and inputs. Consider a function that takes two numbers and adds them:

% mySum.m
function aPb = mySum(a, b)
    aPb = a + b;
end

Save the above function as mySum.m and enter mySum(1, 3) in the command window to get the results we expected. In this case, because there is only one variable to be output, aPb, [] could be omitted, but in the case of a function that outputs multiple variables, you must use [].

% mySumMul.m
function [aPb, aTb] = mySumMul(a, b)
    aPb = a + b;
    aTb = a * b;
end

This function can also be saved as a script file and loaded as mySumMul(3, 4) in the command window. In this case, unless otherwise specified, the function always outputs only the first output variable (aPb). If you want to get both results, you need to match each of the variables to be assigned like [x, y] = mySumMul(3, 4).

Exercises

Write a function that takes an arbitrary square matrix and outputs the determinant.
[Hint: Matlab functions can be written by calling itself, recurrently. Observe that the co-factor expansion has natural recursive form.]
Write a function myRREF that finds the RREF of a given matrix.

Writing a function to find the RREF for an arbitrary matrix is a bit complicated. Here, write a function that works only for matrices that can apply the Gaussian elimination method without using the third elementary row operation, the ‘row exchange’. You can find a matrix like this in exercise 6 in textbook 2.1.
Referring to problem 2, write a function that does \(LU\)-decomposition for matrices that can apply the Gaussian elimination method without using the third elementary row operation, the ‘row exchange’.

Share on

Twitter Facebook

MATLAB TA

Assignment 4

과제 4

0. 연습문제 해설

0.1. 과제 2. 연습문제

0.2. 과제 3. 연습문제

1. `if` 조건문

1.1. 간단한 `if` 조건문

1.2. `if-else` 조건문

1.3. `if-elseif-else` 조건문

2. `continue`와 `break`

3. `function`의 작성

연습문제

Assignment 4

0. Solution to exercises

0.1. Exercises, assignment 2

0.2. Exercises, assignment 3

1. `if` conditional statement

1.1. a simple `if` statement

1.2. `if-else` statement

1.3. `if-elseif-else` statement

2. `continue`and `break`

3. `function` file

Exercises

Share on

Leave a comment

MATLAB TA

과제 4

0. 연습문제 해설

0.1. 과제 2. 연습문제

0.2. 과제 3. 연습문제

1. if 조건문

1.1. 간단한 if 조건문

1.2. if-else 조건문

1.3. if-elseif-else 조건문

2. continue와 break

3. function의 작성

연습문제

Assignment 4

0. Solution to exercises

0.1. Exercises, assignment 2

0.2. Exercises, assignment 3

1. if conditional statement

1.1. a simple if statement

1.2. if-else statement

1.3. if-elseif-else statement

2. continueand break

3. function file

Exercises

Share on

Leave a comment

1. `if` 조건문

1.1. 간단한 `if` 조건문

1.2. `if-else` 조건문

1.3. `if-elseif-else` 조건문

2. `continue`와 `break`

3. `function`의 작성

1. `if` conditional statement

1.1. a simple `if` statement

1.2. `if-else` statement

1.3. `if-elseif-else` statement

2. `continue`and `break`

3. `function` file